【中学受験】有名中学現役教諭の”数学”特別授業~「音楽と算数」新しい曲は無限に作れるのか?〜

有名中の授業は、好奇心をくすぐる仕掛けが盛りだくさん。そして、学ぶことの本質を突いた授業は、探求心あふれる生徒を育てます。さあ、あなたも知的な冒険に出かけましょう!
「音楽と算数」〜新しい曲は無限に作れるのか?〜
執筆:北嶺中・高等学校 数学科教諭 小刀禰 幹朗
みなさんは、生活の中で音楽を聴きますか?
きっと、テレビやラジオ、YouTubeなどで、毎日のように音楽を耳にしていると思います。
最近は、たくさんの歌手やグループが、新しい曲を世界中で発表していますよね。
でも、こんなふうに思ったことはありませんか?
「毎日のように新しい曲が発表されているのに、よく同じような曲ばかりにならないなぁ」
たしかに、似たようなメロディーやリズムの曲があって話題になることもありますが、
それでも、私たちは毎日、新しい音楽を楽しんでいます。
では、どうしてこんなにたくさんの曲が作れるのでしょうか?
そもそも、新しい曲って、無限に作れるものなんでしょうか?
今回は、音楽の「音階の組み合わせ」を使って、それを算数の考え方で調べてみることにしました。
① 音階(おんかい)って、いくつあるの?
音楽は、「ドレミファソラシド」などの「音の高さ(音階)」を組み合わせて作られています。
実は、よく使われる音階には、12個の音があります。たとえば:
ド、ド♯(シャープ)、レ、レ♯、ミ、ファ、ファ♯、ソ、ソ♯、ラ、ラ♯、シ
この12個の音を使って、メロディーが作られているんですね。
② 組み合わせって、どれくらいあるの?
ここからは、算数の力を使って考えてみます。
「1オクターブ」(13個の音)だけを使って、4拍子の1小節分で、どれだけの組み合わせがあるのか調べてみました。
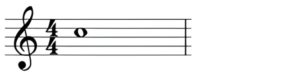
(1)全音符が1つのとき
音は13個なので、
13通り
(2)2分音符が2つのとき
13 × 13 = 169通り

(3)付点2分音符と4分音符が1つずつのとき
順番もあるので、
13 × 13 × 2 = 338通り

(4)2分音符1つ+4分音符2つのとき
順番は3通りなので、
13 × 13 × 13 × 3 = 6,591通り

(5)4分音符が4つのとき
13 × 13 × 13 × 13 = 28,561通り

どうでしょうか?
たった1小節、1オクターブの中だけを使っても、これだけのパターンがあります。
さらに…
など、音の長さやリズムの工夫をすると、組み合わせは何億通りにもなります。
つまり、新しい曲は、ほぼ「無限」に近く作れるということが分かります。
③ それでも似た曲があるのはなぜ?
こんなにたくさんの組み合わせがあるのに、なぜ「似たような曲」が生まれるのでしょうか?
それは、よく使われるパターンが決まっているからです。
たとえば:
つまり、実際に使われているパターンは限られているので、似た曲も生まれてしまうのです。
④ でも、音楽はまだまだ作れる!
それでも、音の高さだけでなく、
などを自由に組み合わせて工夫すれば、新しい音楽はまだまだ無限に近く作ることができます。
音楽と算数は、一見関係なさそうですが、「組み合わせを考える」という意味では、とても深いつながりがあります。
音階の数、音の順番、リズム、コードなどを算数のように数えてみると、
「どうして新しい曲がたくさん作れるのか?」がよくわかります。
これから音楽を聴くときには、ちょっとだけ算数の視点も持ってみると、
もっと音楽が楽しく感じられるかもしれませんね。
株式会社浜学園




